Applicazioni dell’algebra

Temi correlati:
Altre lezioni per il GRE Math, fogli di lavoro di matematica
Questa lezione fa parte di una serie di lezioni per la sezione di ragionamento quantitativo del test generale rivisto GRE. In questa lezione impareremo:

• Applicazioni dell’Algebra
• Tradurre le parole in Algebra
• Esempi di utilizzo dell’Algebra per risolvere problemi di parole
  • Problemi di media
  • Problemi di parole miste
  • Distanza, tasso, Time Word Problems
  • Work Word Problems
  • Word Problems that involve Simultaneous Equations
  • Word Problems that involve Inequalities

Applicazioni dell’Algebra
Tradurre le descrizioni verbali in espressioni algebriche è un passo iniziale essenziale nella risoluzione dei problemi di parole.
Di seguito sono riportati alcuni esempi.
– Se il quadrato del numero x viene moltiplicato per 4, e poi 15 viene aggiunto a quel prodotto, il risultato può essere rappresentato da 4×2 + 15
– Se l’attuale stipendio s di Peter viene aumentato del 15%, allora il suo nuovo stipendio è 1,15s.
– Se y galloni di succo d’arancia devono essere distribuiti tra 5 persone in modo che una persona in particolare riceva 1 gallone e il resto del succo sia diviso equamente tra le altre 4, allora ognuna di queste 4 persone riceverà (y – 1) ÷ 4
Questo video mostra come tradurre parole ed espressioni in espressioni algebriche che coinvolgono variabili.

• Mostra le soluzioni passo dopo passo

Esempi di utilizzo di tecniche algebriche per risolvere problemi di parole
Vi mostreremo ora alcuni esempi di utilizzo di tecniche algebriche per risolvere problemi di parole. Altri esempi di problemi di parole algebrici possono essere trovati qui. Problemi di parole sulla media

Questi sono esempi di problemi di parole che coinvolgono la media o la media aritmetica.

Esempio 1:

Ellen ha ricevuto i seguenti punteggi su 3 esami: 82, 74, e 90. Quale punteggio
Ellen dovrà ricevere nel prossimo esame in modo che la media (media aritmetica) dei 4 esami sia 85?
Lascia che x rappresenti il punteggio del prossimo esame di Ellen.
La media dei 4 esami è

Solvendo per x otteniamo

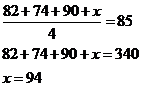
Pertanto, Ellen dovrà raggiungere un punteggio di 94 al prossimo esame.

Esempio 2:

Nelle sue prime quattro partite Jennifer ha lanciato 101, 112, 126, 108. Qual è il punteggio minimo che deve fare nella sua quinta partita per avere una media di almeno 110?

• Mostra le soluzioni passo dopo passo

Problemi di parole sulle miscele

Questi sono alcuni esempi di problemi di parole che riguardano le miscele e la concentrazione di miscele.

Esempio 1:
Una miscela di 12 once di aceto e olio è il 40% di aceto, dove tutte le
misure sono in peso. Quante once di olio devono essere aggiunte alla miscela per produrre una nuova miscela che è solo il 25% di aceto?
Lasciate che x rappresenti il numero di once di olio da aggiungere. Allora il numero totale di once della nuova miscela sarà 12 + x, e il numero totale di once di aceto nella nuova miscela sarà (0,40)(12). Dato che la nuova miscela deve essere il 25% di aceto, otteniamo

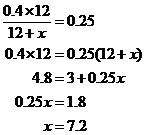
7,2 once di olio devono essere aggiunte per produrre una nuova miscela che sia il 25% di aceto.

Esempio 2:

Una soluzione contiene 15% di acido cloridrico. Quanta acqua deve essere aggiunta a 50 ml di questa soluzione per diluirla al 2%?

• Mostra le soluzioni passo dopo passo

Problemi di distanza, velocità, tempo

Questi sono alcuni esempi di problemi di distanza, velocità, tempo.

Esempio 1:

In una gara di guida, Jeff e Dennis hanno guidato sullo stesso percorso a una velocità media di 51
miglia all’ora e 54 miglia all’ora, rispettivamente. Se Jeff ha impiegato 40 minuti per percorrere il percorso, quanto tempo ha impiegato Dennis?
Lascia che x sia il tempo, in minuti, che Dennis ha impiegato per percorrere il percorso. La distanza d, in miglia, è uguale al prodotto della velocità r, in miglia all’ora, e il tempo t, in ore; cioè, d = rt
Nota che poiché le velocità sono date in miglia all’ora, è necessario esprimere i tempi in ore; per esempio, 40 minuti equivalgono di un’ora.
Utilizzando la formula, d = rt, possiamo ottenere la seguente tabella.

	Distanza	Rate	Time
Jeff	51 ×
Dennis	54 ×

Siccome le distanze sono uguali,

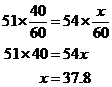
Dennis ha impiegato circa 37.8 minuti per percorrere il percorso.

Un’introduzione alla risoluzione di problemi di moto uniforme (velocità-tempo-distanza) usando la formula velocità x tempo = distanza, o rt=d.
Esempio:
Due ciclisti partono dallo stesso angolo e vanno in direzioni opposte. Un ciclista va due volte più veloce dell’altro. In 3 ore, si trovano a 81 miglia di distanza. Trova la velocità di ciascun ciclista. Risposta: 9 mph e 18 mph.

• Mostra le soluzioni passo dopo passo

Problema di parola usando la formula del moto uniforme rt=d
Esempio:
Un corridore ha iniziato a correre ad una velocità media di 6 mph. Mezz’ora dopo, un altro corridore ha iniziato a correre dopo di lui partendo dallo stesso posto ad una velocità media di 7 mph. Quanto tempo impiegherà il corridore a raggiungere il jogger? Risposta: 3 ore.

• Mostra le soluzioni passo per passo

Problema di parola usando la formula del moto uniforme rt=d
Esempio:
Un viaggio di 555 miglia e 5 ore sull’Autobahn è stato fatto a due velocità. La velocità media dell’auto era di 105 mph nella prima parte del viaggio, e la velocità media era di 115 mph per la seconda parte. Per quanto tempo l’auto ha viaggiato ad ogni velocità? Risposta: 105 mph per 2 ore e 115 mph per 3 ore.

• Mostra le soluzioni passo per passo

Problema di parola usando la formula del moto uniforme rt=d

Esempio:
Andy e Beth sono alle estremità opposte di una strada di campagna di 18 miglia con l’intenzione di partire allo stesso tempo correndo verso l’altro per incontrarsi. Andy corre a 7 mph mentre Beth corre a 5 mph. Quanto tempo dopo il loro inizio si incontreranno? Risposta: 1,5 ore.

• Mostra le soluzioni passo dopo passo

Esempio:
Un’auto e un autobus partono alle 14:00 dallo stesso punto, diretti nella stessa direzione. La velocità media dell’auto è il doppio della velocità media dell’autobus. Dopo 2 ore, l’auto è 68 miglia avanti all’autobus. Trova la velocità dell’autobus e dell’auto. Risposta: Velocità dell’autobus: 34 mph; Velocità dell’auto: 68 mph.

• Mostra le soluzioni passo dopo passo

Esempio:
Un pilota ha volato da una città a un’altra città a una media di 150 mph. Più tardi, è tornato indietro alla prima città con una media di 100 mph. Il tempo totale di volo è stato di 5 ore. Quanto distano le città? Risposta: 300 miglia

• Mostra le soluzioni passo per passo

Problemi di parole sul lavoro
Questi sono alcuni esempi di problemi di parole che riguardano il lavoro svolto da individui o macchine.
Esempio:
Maria impiega dieci ore per raccogliere quaranta mele. Kayla può raccogliere la stessa quantità in 12 ore. Quanto tempo impiegherebbero se lavorassero insieme?

• Mostra le soluzioni passo per passo

Problemi di parole che implicano lavoro
Esempi:
1. Un pittore esperto impiega 6 giorni per dipingere una casa. Un apprendista impiega 8 giorni per dipingere la stessa casa. Quanto tempo ci vorrebbe se lavorassero insieme?
2. Un tubo può riempire un serbatoio in 8 ore. Un altro tubo può svuotare il serbatoio in 12 ore. Se entrambi i tubi vengono aperti simultaneamente, quanto tempo ci vorrà per riempire il serbatoio?

• Mostra le soluzioni passo per passo

Applicazioni che coinvolgono sistemi di equazioni
I seguenti sono esempi di applicazioni che coinvolgono sistemi di equazioni o la risoluzione di equazioni simultanee.
Esempi:
1. Trova due numeri la cui somma è 93 e la differenza è 9.
2. Il perimetro di un rettangolo è 160 yd. La larghezza è 4 più della metà della lunghezza. Trova la lunghezza e la larghezza.
3. Sunset affitta un camion da 18 piedi per 49,95 dollari più 75 centesimi a miglio. Cactus affitta un furgone da 18 piedi per $59.95 più 50 centesimi per miglio. Per quale chilometraggio il costo è lo stesso?

• Mostra le soluzioni passo dopo passo

Esempi:
1. Supponiamo che tutti i corsi del Pheonix College valgano 3 o 4 crediti. La squadra di corsa campestre sta seguendo un totale di 40 corsi che valgono 144 crediti. Quanti corsi da 3 crediti e quanti corsi da 4 crediti vengono seguiti?
2. HomeMart fa pagare 3,50 dollari per una lampadina CFL e Supply Depot fa pagare 2,50 dollari per una lampadina CFL che non dura così tanto. Se il tuo condominio ha perso la fattura, ma sanno di aver acquistato 300 lampadine e speso 885 dollari, quante lampadine sono state acquistate da ciascun negozio.
3. Grounds Works addebita $8.00/lb per il caffè premium roast e $4.50/lb per il caffè value roast. Quanto di ogni tipo dovrebbe essere usato per fare una miscela 10lb che costerebbe $5.90/lb?
4. Un treno lascia Prescott, AZ e viaggia verso nord al Grand Canyon ad una velocità di 25mph. Un’ora e mezza dopo, un treno espresso parte su un binario parallelo e viaggia verso nord a 60 mph. Quanto lontano dalla stazione di partenza si incontreranno?

• Mostra le soluzioni passo dopo passo

Applicazioni che coinvolgono disuguaglianze
I seguenti sono esempi di problemi di algebra che coinvolgono disuguaglianze
Esempi:
1. Andrea ha $53.50 in tasca e vuole acquistare delle camicie al prezzo di vendita di $14.95 ciascuna.
Qual è il maggior numero di camicie che può comprare? (Supponiamo che le camicie siano esenti dall’imposta sulle vendite)
2. Tre volte un numero aumentato di 8 è al massimo 40. Trova il più grande valore possibile del numero.
3. La lunghezza di un rettangolo è 8 metri meno di 5 volte la sua larghezza. Se il perimetro del rettangolo è al massimo 104 metri, trova la massima larghezza possibile del rettangolo.
4. Due numeri consecutivi sono tali che la loro somma è maggiore di 98 diminuita del doppio del più grande. Trova i più piccoli valori possibili per i numeri interi.

• Mostra le soluzioni passo per passo

Esempio:
Una fabbrica di widget ha un costo operativo fisso di $3.600 al giorno più i costi di $1.40 per ogni widget prodotto. Se un widget viene venduto a 4,20 dollari, qual è il numero minimo di widget che devono essere venduti al giorno per ottenere un profitto?

• Mostra le soluzioni passo dopo passo

Prova la calcolatrice gratuita Mathway e il risolutore di problemi qui sotto per praticare vari argomenti di matematica. Prova gli esempi dati, o scrivi il tuo problema e controlla la tua risposta con le spiegazioni passo dopo passo.