Sistema cristallino ortorombico

Celle unitarie rettangolari contro rombiche per i reticoli 2D ortorombici. Lo scambio del tipo di centratura quando si cambia la cella unitaria si applica anche per i tralicci ortoombici 3D

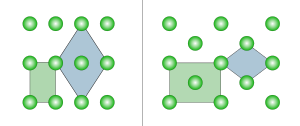
Two-dimensionalEdit

In due dimensioni ci sono due tralicci Bravais ortorombici: rettangolare primitivo e rettangolare centrato. Il reticolo rettangolare primitivo può anche essere descritto da una cella unitaria rombica centrata, mentre il reticolo rettangolare centrato può anche essere descritto da una cella unitaria rombica primitiva.

Modifica tridimensionale

In tre dimensioni, ci sono quattro reticoli Bravais ortorombici: ortorombico primitivo, ortorombico a base centrata, ortorombico a corpo centrato e ortorombico a faccia centrata.

Lattice di Bravais	Primitiva ortorombica	Base-centrato ortorombico	Centrato sul corpo ortorombico	Faccia-centrato ortorombico
Simbolo di Pearson	oP	oS	oI	oF
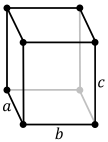
Cella unitaria standard
Prisma rombico retto cella unitaria

Nel sistema ortorombico esiste una seconda scelta di assi cristallini, raramente utilizzata, che dà come risultato una cella unitaria a forma di prisma rombico destro; può essere costruita perché lo strato di base rettangolare bidimensionale può anche essere descritto con assi rombici. In questa impostazione degli assi, i tralicci primitivi e quelli centrati sulla base si scambiano il tipo di centratura, mentre la stessa cosa accade con i tralicci centrati sul corpo e quelli centrati sulla faccia. Notate che la lunghezza a {\displaystyle a}

nella riga inferiore non è la stessa della riga superiore, come si può vedere nella figura nella sezione sui reticoli bidimensionali. Per la prima e la terza colonna di cui sopra, a {\displaystyle a}

della seconda riga è uguale a 2 + b 2 {\displaystyle {\sqrt {a^{2}+b^{2}}}}

della prima riga, e per la seconda e quarta colonna è uguale alla metà di questa.