MathematikPreCalculus Mathematik in Nebraska
AbschnittHorizontale Dehnungen und Stauchungen
Im vorherigen Abschnitt haben wir das Ergebnis der Multiplikation der Ausgabe der Funktion mit einem konstanten Wert besprochen. Was passiert jedoch, wenn wir die Eingabe der Funktion multiplizieren? Um diese Idee zu untersuchen, betrachten wir die Graphen von
und diskutieren, wie sie zusammenhängen.
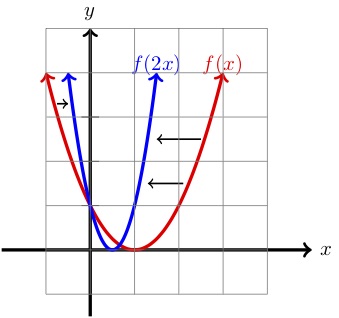
| \(x\) | \(y=f(x)\) | \(y=f(2x)\) | |
| \(-1\) | \(4\) | \(8\) | |
| \(-.5\) | \(2,25\) | \(4\) | |
| \(0\) | \(1\) | \(1\) | |
| \(.5\) | \(.25\) | \(0\) | |
| \(1\) | \(0\) | \(1\) | |
| \(2\) | \(1\) | \(9\) |
Wie wir oben sehen können, im Vergleich zum Graphen von \(f(x)\text{,}\) ist der Graph von \(f(2x) \) horizontal um einen Faktor von \(2 \text{.}\) Effektiv, wenn wir einen Punkt \((x,y) \) auf dem Graphen von \(f(x) \) gegeben sind, dann ist \(\(\dfrac{1}{2}x,y\right) \) ein Punkt auf dem Graphen von \(f(2x)\text{.}\)
Betrachten wir die obige Tabelle, können wir dies für ein paar Punkte verifizieren. Zum Beispiel liegt der Punkt \((2,1)\) auf dem Graphen von \(f(x)\text{.}\) Dann
ist ein Punkt auf dem Graphen \(f(2x)\text{.}\)
Horizontale Streckung
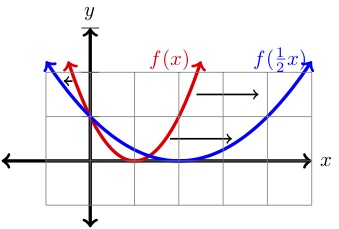
| \(x\) | \(y=f(x)\) | \(y=f\links(\dfrac{1}{2}x\rechts)\) | \(-1\) | \(4\) | \(2.25\) |
| \(0\) | \(1\) | \(1\) | |
| \(1\) | \(0\) | \(.25\) | |
| \(2\) | \(1\) | \(0\) | |
| \(4\) | \(9\) | \(1\) |
Der Graph von \(f\left(\dfrac{1}{2}x\right)\) ist horizontal um den Faktor \(2 \) gestreckt im Vergleich zum Graph von \(f(x) \text{.}\) Wenn \((x,y) \) ein Punkt auf dem Graphen von \(f(x)\text{,}\) ist, dann ist \((2x,y) \) ein Punkt auf dem Graphen von \(f\left(\dfrac{1}{2}x\right)\text{.}\)
Wir können dies in unserem Beispiel oben sehen. Beachten Sie, dass \((2,1) \) ein Punkt auf \(f(x)\text{,}\) ist und
ein Punkt auf dem Graphen von \(f\left(\dfrac{1}{2}xright)\) ist, wie in der Tabelle und dem Graphen oben gezeigt. Im Allgemeinen haben wir:
Horizontale Dehnungen, Stauchungen und Spiegelungen
Verglichen mit dem Graphen von \(y = f (x)\text{,}\) ist der Graph von \(y = f (a\cdot x)\text{,}\), wobei \(a \ne 0\text{,}\) horizontal um einen Faktor von \(\abs{a}\) komprimiert ist, wenn \(\abs{a}\gt 1\text{,}\)
Wie Sie vielleicht schon anhand unserer Beispiele bemerkt haben, wird eine horizontale Streckung oder Stauchung niemals die \(y\)-Achsenabschnitte verändern. Dies ist eine gute Möglichkeit zu erkennen, ob eine solche Transformation stattgefunden hat.
Beispiel272
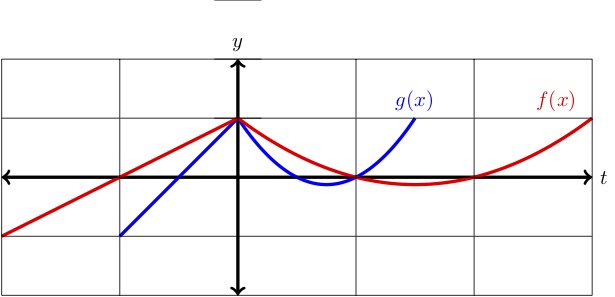
Der Graph von \(f(x)\) wird zusammen mit einer horizontalen Streckung oder Stauchung von \(f(x) \text{.}\) Entscheiden Sie, ob \(g(x) \) eine Streckung oder eine Stauchung ist, und geben Sie eine Formel für \(g(x)\) in Bezug auf \(f(x)\text{.}\)
Lösung
Erstens, beachten Sie, dass der \(y\)-Abschnittpunkt fest bleibt, während sich die \(x\)-Abschnitte näher zur \(y\)-Achse verschieben. Dies sagt uns, dass \(g(x)\) eine horizontale Kompression ist. Die \(x\)-Abschnitte von \(f(x)\) sind \(x=-1,1,2 \), während die \(x\)-Abschnitte von \(g(x)\) \(x=-.5,.5,1\text{.})
Die \(x\)-Abschnitte von \(g(x) \) erhält man also, indem man die Abschnitte von \(f(x) \) nimmt und jeweils durch 2 teilt. Das sagt uns, dass \(g(x)\) eine horizontale Kompression um den Faktor \(2 \text{.}\) Daher können wir schreiben