Orthorhombisch kristalsysteem

Rechthoekige vs rhombische eenheidscellen voor de 2D orthorhombische roosters. Het verwisselen van centreringstype bij verandering van de eenheidscel geldt ook voor de 3D orthorhombische roosters

TweedimensionaalEdit

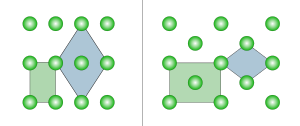
In twee dimensies zijn er twee orthorhombische Bravais-roosters: primitief rechthoekig en gecentreerd rechthoekig. Het primitieve rechthoekige rooster kan ook beschreven worden door een gecentreerde ruitvormige eenheidscel, terwijl het gecentreerde rechthoekige rooster ook beschreven kan worden door een primitieve ruitvormige eenheidscel.

DriedimensionaalEdit

In drie dimensies zijn er vier orthorhombische Bravais-roosters: primitief orthorhombisch, basisgecentreerd orthorhombisch, lichaamsgecentreerd orthorhombisch, en aangezichtsgecentreerd orthorhombisch.

.gecentreerd
orthorhombisch

Bravais-rooster	Primitief orthorhombisch	Basis-gecentreerd orthorhombisch	Primitief orthorhombisch	Basis-gecentreerd orthorhombisch	lichaamsgecentreerd orthorhombisch	Face-gecentreerd orthorhombisch
Pearson symbool	oP	oS	oI	oF
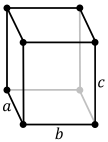
Standaard eenheidscel
Recht ruitvormig prisma eenheidscel

In het orthorhombische stelsel is er een zelden gebruikte tweede keuze van kristalassen die resulteert in een eenheidscel met de vorm van een rechts rhombisch prisma; deze kan worden geconstrueerd omdat de rechthoekige tweedimensionale basislaag ook kan worden beschreven met rhombische assen. In deze assenstelling wisselen de primitieve en basis-gecentreerde roosters elkaar af in centreringstype, terwijl hetzelfde gebeurt met de lichaamsgecentreerde en gezichtsgecentreerde roosters. Merk op dat de lengte a {displaystyle a}

in de onderste rij niet dezelfde is als in de bovenste rij, zoals te zien is in de figuur in het gedeelte over tweedimensionale roosters. Voor de eerste en derde kolom hierboven is a {displaystyle a}

van de tweede rij gelijk aan a 2 + b 2 {{displaystyle {\sqrt {a^{2}+b^{2}}}}

van de eerste rij, en voor de tweede en vierde kolom is het gelijk aan de helft hiervan.