Toepassingen van Algebra

Onderwerpen die hiermee verband houden:
Meer lessen voor GRE Math, Math Worksheets
Deze les maakt deel uit van een serie lessen voor het onderdeel kwantitatief redeneren van de GRE revised General Test. In deze les leren we:

• Toepassingen van Algebra
• Woorden vertalen naar Algebra
• Voorbeelden van het gebruik van Algebra om woordproblemen op te lossen
  • Gemiddelde woordproblemen
  • Gemengde woordproblemen
  • Verstand, Snelheid,
  • Werkwoordproblemen
  • Woordproblemen met gelijktijdige vergelijkingen
  • Woordproblemen met ongelijkheden

Toepassingen van Algebra
Het vertalen van mondelinge beschrijvingen in algebraïsche uitdrukkingen is een essentiële eerste stap bij het oplossen van woordproblemen.
Hiervan volgen enkele voorbeelden.
– Als het kwadraat van het getal x wordt vermenigvuldigd met 4, en dan 15 wordt opgeteld bij dat product, dan kan het resultaat worden weergegeven als 4×2 + 15
– Als Peters huidige salaris s wordt verhoogd met 15 procent, dan is zijn nieuwe salaris 1,15s.
– Als y liter sinaasappelsap moet worden verdeeld over 5 mensen, zodat één persoon 1 liter krijgt en de rest van het sap gelijkelijk wordt verdeeld over de overige 4, dan krijgt elk van die 4 mensen (y – 1) ÷ 4
Deze video laat zien hoe je woorden en uitdrukkingen vertaalt in algebraïsche uitdrukkingen met variabelen.

• Laat stap-voor-stap oplossingen zien

Voorbeelden van het gebruik van algebraïsche technieken om woordproblemen op te lossen
We zullen nu een aantal voorbeelden laten zien van het gebruik van algebraïsche technieken om woordproblemen op te lossen. Meer voorbeelden van algebraïsche woordproblemen zijn hier te vinden. Gemiddelde woordproblemen

Hieronder staan voorbeelden van woordproblemen waarbij het gemiddelde of rekenkundig gemiddelde een rol speelt.

Voorbeeld 1:

Ellen heeft op 3 examens de volgende scores gehaald: 82, 74, en 90. Welke score moet
Ellen op het volgende examen halen, zodat de gemiddelde (rekenkundig gemiddelde) score voor de 4 examens 85 is?
Laat x staan voor de score op Ellens volgende examen.
Het gemiddelde van de 4 examens is

Oplossen voor x krijgen we

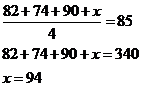
Daarom zal Ellen op het volgende examen een score van 94 moeten halen.

Voorbeeld 2:Op haar eerste vier games bowlde Jennifer 101, 112, 126, 108. Wat is de minimumscore die ze in haar vijfde game moet gooien om een gemiddelde van minstens 110 te halen?

• Stapsgewijze oplossingen tonen

Woordproblemen met mengsels

Hieronder volgen enkele voorbeelden van woordproblemen waarbij het gaat om mengsels en concentraties van mengsels.

Voorbeeld 1:
Een mengsel van 12 ons azijn en olie is 40 procent azijn, waarbij alle
maten naar gewicht zijn. Hoeveel gram olie moet er aan het mengsel worden toegevoegd om een nieuw mengsel te krijgen dat nog maar voor 25 procent uit azijn bestaat?
Laat x het aantal grammen olie zijn dat moet worden toegevoegd. Het totale aantal grammen van het nieuwe mengsel is dan 12 + x, en het totale aantal grammen azijn in het nieuwe mengsel is (0,40)(12). Omdat het nieuwe mengsel voor 25 procent uit azijn moet bestaan, krijgen we

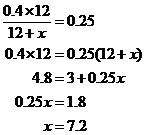
7,2 ons olie moet worden toegevoegd om een nieuw mengsel te krijgen dat voor 25 procent uit azijn bestaat.

Voorbeeld 2:

Een oplossing bevat 15 procent zoutzuur. Hoeveel water moet aan 50 ml van deze oplossing worden toegevoegd om het te verdunnen tot een oplossing van 2%?

• Stapsgewijze oplossingen tonen

Verstand, snelheid, tijd woordproblemen

Hieronder staan enkele voorbeelden van afstand, snelheid, tijd woordproblemen.

Voorbeeld 1:

In een rijwedstrijd hebben Jeff en Dennis hetzelfde parcours afgelegd met een gemiddelde snelheid van respectievelijk 51 en 54 mijl per uur. Als Jeff er 40 minuten over deed om het parcours af te leggen, hoe lang deed Dennis er dan over?
Laat x de tijd zijn, in minuten, die Dennis nodig had om het parcours af te leggen. De afstand d, in mijlen, is gelijk aan het product van de snelheid r, in mijlen per uur, en de tijd t, in uren; dat is, d = rt
Merk op dat omdat de snelheden in mijlen per uur gegeven zijn, het nodig is om de tijden in uren uit te drukken; bijvoorbeeld, 40 minuten is gelijk aan van een uur.
Met de formule, d = rt, krijgen we de volgende tabel.

	Afstand	Tarief	Tijd
Jeff	51 ×
Dennis	54 ×

Omdat de afstanden gelijk zijn,

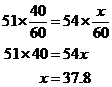
Het kostte Dennis ongeveer 37.8 minuten om het parcours af te leggen.

Een inleiding tot het oplossen van woordproblemen over eenparige beweging (snelheid-tijd-afstand) met behulp van de formule snelheid x tijd = afstand, of rt=d.
Voorbeeld:
Twee fietsers beginnen op dezelfde hoek en rijden in tegengestelde richting. De ene fietser rijdt twee keer zo snel als de andere. In 3 uur zijn ze 81 mijl van elkaar verwijderd. Bereken de snelheid van elke fietser. Antwoord: 9 mph en 18 mph.

• Stap voor stap oplossingen laten zien

Woordprobleem met behulp van uniforme beweging rt=d formule
Voorbeeld:
Een jogger begon te rennen met een gemiddelde snelheid van 6 mph. Een half uur later begint een andere jogger vanaf dezelfde plaats achter hem aan te rennen met een gemiddelde snelheid van 7 km/uur. Hoe lang duurt het voordat de hardloper de jogger heeft ingehaald? Antwoord: 3 uur.

• Stap voor stap oplossingen laten zien

Woordprobleem met behulp van uniforme beweging rt=d formule
Voorbeeld:
Een reis van 555 mijl en 5 uur over de Autobahn werd gereden met twee snelheden. De gemiddelde snelheid van de auto was 105 km/u op het eerste deel van de reis, en de gemiddelde snelheid was 115 km/u voor het tweede deel. Hoe lang reed de auto bij elke snelheid? Antwoord: 105 mph gedurende 2 uur en 115 mph gedurende 3 uur.

• Stap voor stap oplossingen laten zien

Woordprobleem met behulp van uniforme beweging rt=d formule
Voorbeeld:
Andy en Beth staan aan tegenovergestelde uiteinden van een landweg van 18 mijl met plannen om op hetzelfde moment te vertrekken en naar elkaar toe te rennen om elkaar te ontmoeten. Andy loopt 7 km/uur terwijl Beth 5 km/uur loopt. Hoe lang nadat ze zijn begonnen zullen ze elkaar ontmoeten? Antwoord: 1,5 uur.

• Stap-voor-stap oplossingen tonen

Voorbeeld:
Een auto en een bus vertrekken om 14.00 uur vanaf dezelfde plek, in dezelfde richting. De gemiddelde snelheid van de auto is twee keer zo hoog als de gemiddelde snelheid van de bus. Na 2 uur ligt de auto 68 mijl voor op de bus. Bereken de snelheid van de bus en de auto. Antwoord: Snelheid van de bus: 34 mph; Snelheid van de auto: 68 mph.

• Stapsgewijze oplossingen tonen

Voorbeeld:
Een piloot vloog van de ene stad naar de andere stad met een gemiddelde snelheid van 150 mijl per uur. Later vloog hij terug naar de eerste stad met een gemiddelde snelheid van 100 mijl per uur. De totale vliegtijd was 5 uur. Hoe ver liggen de steden uit elkaar? Antwoord: 300 mijl

• Stapsgewijze oplossingen tonen

Werkwoordproblemen
Hier volgen enkele voorbeelden van woordproblemen waarbij het gaat om werk dat door individuen of machines wordt gedaan.
Voorbeeld:
Het kost Maria tien uur om veertig schepels appels te plukken. Kayla kan dezelfde hoeveelheid in 12 uur plukken. Hoe lang zouden ze erover doen als ze samenwerkten?

• Stapsgewijze oplossingen tonen

Woordproblemen met werk
Voorbeelden:
1. Een ervaren schilder heeft 6 dagen nodig om een huis te schilderen. Een leerling doet er 8 dagen over om hetzelfde huis te schilderen. Hoe lang zou het duren als ze samenwerkten?
2. Een pijp kan een tank in 8 uur vullen. Een andere pijp kan de tank in 12 uur legen. Als beide pijpen tegelijk worden geopend, hoe lang duurt het dan om de tank te vullen?

• Stapsgewijze oplossingen tonen

Toepassingen waarbij stelsels van vergelijkingen een rol spelen
Hieronder volgen voorbeelden van toepassingen waarbij stelsels van vergelijkingen een rol spelen of waarbij gelijktijdige vergelijkingen worden opgelost.

Voorbeelden:
1. Zoek twee getallen waarvan de som 93 is en het verschil 9.
2. De omtrek van een rechthoek is 160 yd. De breedte is 4 meer dan de helft van de lengte. Bereken de lengte en de breedte.
3. Sunset huurt een vrachtauto van 1,80 m voor 49,95 dollar plus 75 cent per mijl. Cactus huurt een bestelwagen van 18 ft voor $ 59,95 plus 50 cent per mijl. Voor welke kilometerstand zijn de kosten gelijk?

• Stapsgewijze oplossingen tonen

Voorbeelden:
1. Veronderstel dat alle cursussen van het Pheonix College ofwel 3 ofwel 4 studiepunten waard zijn. Het cross country team volgt in totaal 40 cursussen die 144 studiepunten waard zijn. Hoeveel vakken van 3 studiepunten en hoeveel vakken van 4 studiepunten worden er gevolgd?
2. HomeMart rekent $3,50 voor een CFL gloeilamp en Supply Depot rekent $2,50 voor een CFL gloeilamp die niet zo lang meegaat. Als uw appartementencomplex de rekening kwijt is, maar wel weet dat ze 300 lampen hebben gekocht en 885 dollar hebben uitgegeven, hoeveel lampen zijn er dan bij elke winkel gekocht.
3. Grounds Works rekent 8,00 dollar per pond voor premium roast koffie en 4,50 dollar per pond voor value roast koffie. Hoeveel van elk type moet er gebruikt worden om een melange van 10 pond te maken die 5,90 dollar per pond kost?
4. Een trein vertrekt uit Prescott, AZ en rijdt met een snelheid van 25 km/uur in noordelijke richting naar Grand Canyon. Anderhalf uur later vertrekt een sneltrein over een parallel spoor en rijdt met een snelheid van 60 km/uur naar het noorden. Hoe ver van het beginstation zullen ze elkaar ontmoeten?

• Stapsgewijze oplossingen tonen

Toepassingen waarbij ongelijkheden een rol spelen
De volgende zijn voorbeelden van algebra-woordproblemen waarbij ongelijkheden een rol spelen
Voorbeelden:
1. Andrea heeft $53,50 op zak en wil overhemden kopen tegen een verkoopprijs van $14,95 per stuk.
Wat is het grootste aantal overhemden dat ze kan kopen? (Neem aan dat de overhemden vrijgesteld zijn van omzetbelasting)
2. Drie keer een getal vermeerderd met 8 is maximaal 40. Bereken de grootst mogelijke waarde van het getal.
3. De lengte van een rechthoek is 8 meter kleiner dan 5 keer de breedte. Als de omtrek van de rechthoek ten hoogste 104 meter is, bepaal dan de grootst mogelijke breedte van de rechthoek.
4. Twee opeenvolgende getallen zijn zo dat hun som groter is dan 98 verminderd met tweemaal de grootste. Vind de kleinst mogelijke waarden voor de gehele getallen.

• Stapsgewijze oplossingen tonen

Voorbeeld:
Een widgetfabriek heeft vaste bedrijfskosten van $3.600 per dag plus kosten van $1,40 per geproduceerde widget. Als een widget voor $4,20 wordt verkocht, wat is dan het kleinste aantal widgets dat per dag moet worden verkocht om winst te maken?

• Stapsgewijze oplossingen tonen

Probeer de gratis Mathway rekenmachine en probleemoplosser hieronder om verschillende wiskunde-onderwerpen te oefenen. Probeer de gegeven voorbeelden, of typ je eigen probleem in en controleer je antwoord met de stap-voor-stap uitleg.