WiskundePreCalculus Wiskunde op Nebraska

ParagraafHorizontale strekkingen en compressies

In de vorige paragraaf bespraken we het resultaat van het vermenigvuldigen van de uitgang van de functie met een constante waarde. Maar wat gebeurt er als we de invoer van de functie vermenigvuldigen? Om dit idee te onderzoeken, bekijken we de grafieken van

en bespreken hun onderlinge samenhang.

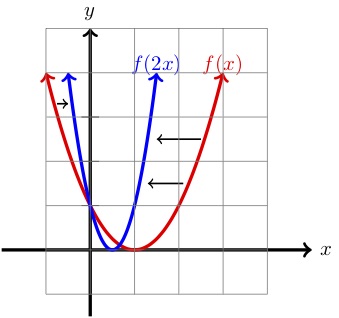
(x)	(y=f(x)\)	(y=f(2x)\)
(x)\)	(y=f(2x)\)	(-)1)	(4)	(8)
(-.5)	(2,25)	(4)
(0)	(1)	(1)
(,5)	(.25)	(0)
(1)	(0)	(1)
(2)	(1)	(9)

Zoals we hierboven kunnen zien, dat in vergelijking met de grafiek van f(x) de grafiek van f(2x) horizontaal is samengedrukt met een factor 2.Als we dus een punt op de grafiek van f(x) krijgen, dan is \links(fdfrac{1}{2}x,yrechts) een punt op de grafiek van f(2x)

In de tabel hierboven kunnen we dit voor een paar punten verifiëren. Bijvoorbeeld, het punt f(2,1) ligt op de grafiek van f(x)\tekst{.}) Dan

is een punt op de grafiek van \(f(2x)\text{.})

Horizontale uitrekking

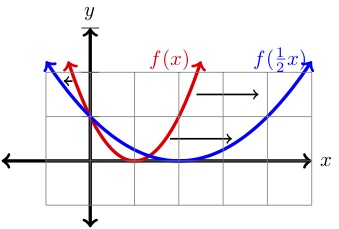
(x)	(y=f(x)\)	(y=f(x)\links(\dfrac{1}{2}x\rechts)\)
(-)1)	(4)	(2..25%
(0)	(1)	(1)
(1)
(1)	(0)	(.25)
(2)	(1)	(0)
(4)	(9)	(1)

De grafiek van f(links(\dfrac{1}{2}xrechts)\) is horizontaal uitgerekt met een factor \(2) vergeleken met de grafiek van f(x) \text{.}\) Verder, als f(x,y) een punt is op de grafiek van f(x)dan is f(2x,y) een punt op de grafiek van f(links)f(f(1}{2}xrechts)f(x)

We kunnen dit zien in ons voorbeeld hierboven. We zien dat f(2,1) een punt is op f(x)en

is een punt op de grafiek van f(f)links(\dfrac{1}{2}xrechts) zoals in de tabel en grafiek hierboven is te zien. In het algemeen hebben we:

Horizontale strekkingen, samendrukkingen en spiegelingen

Vergeleken met de grafiek van \(y = f (x)xtekst{,}) is de grafiek van \(y = f (a\cdot x)xtekst{,) waarbij a 0 is

1. in de breedte samengedrukt met een factor a als a 1 is
3. in de breedte samengedrukt met een factor a als a 1 is
   2. horizontaal uitgerekt met een factor ²(²abs{a}}lt 1) en
   3. gereflecteerd om de y-as (en uitgerekt of samengedrukt) als ²(alt 0}{a}}}).

   Zoals je misschien al door onze voorbeelden hebt gemerkt, zal een horizontale uitrekking of samendrukking nooit de y-raakpunten veranderen. Dit is een goede manier om te zien of zo’n transformatie heeft plaatsgevonden.

   Voorbeeld272

   

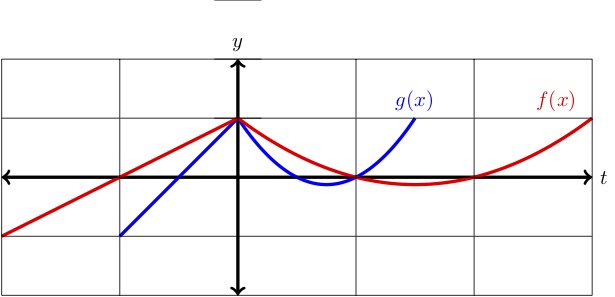
   De grafiek van f(x)wordt getoond samen met ofwel een horizontale uitrekking of compressie van f(x)ofwel een horizontale uitrekking of compressie van f(x)ofwel een horizontale uitrekking of compressie van f(x)ofwel een horizontale uitrekking of compressie van f(x).}\) Bepaal of g(x) een uitrekking of een samendrukking is en geef een formule voor g(x) in termen van f(x).})

   Oplossing

   Eerst, zien we dat het y-asintercept gelijk blijft, terwijl de x-asintercepts dichter naar de y-as verschuiven. Dit vertelt ons dat g(x)een horizontale compressie is. De x-uiteinden van f(x)zijn x=-1,1,2 terwijl de x-uiteinden van g(x)zijn x=-.5,.5,1.

   Dus, de \(x)-uiteinden van \(g(x) \) kunnen worden verkregen door de uiteinden van \(f(x) \) te nemen en elk te delen door 2. Dit vertelt ons dat \(g(x)\) een horizontale compressie is met een factor van \(2 \text{.) Daarom kunnen we

   begin{equation*}g(x)=f(2x).²einde{equation*}

   Oefeningen in subparagraaf

   1Ontdekken van horizontale compressies en uitrekkingen

   2De beschrijving van compressies en uitrekkingen

   3Punten over samendrukkingen en uitrekkingen

   4Grafieken van samendrukkingen en uitrekkingen

   5Domein en bereik van samendrukkingen en uitrekkingen

   6Toepassing: Conversies in Functies