Orthorhombisches Kristallsystem

Rechteckige vs. rhombische Einheitszellen für die 2D-orthorhombischen Gitter. Die Vertauschung des Zentrierungstyps beim Wechsel der Einheitszelle gilt auch für die orthorhombischen 3D-Gitter

ZweidimensionalEdit

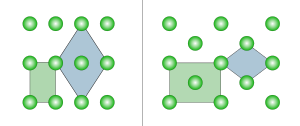
In zwei Dimensionen gibt es zwei orthorhombische Bravais-Gitter: primitiv rechteckig und zentriert rechteckig. Das primitive rechteckige Gitter kann auch durch eine zentrierte rhombische Einheitszelle beschrieben werden, während das zentrierte rechteckige Gitter auch durch eine primitive rhombische Einheitszelle beschrieben werden kann.

DreidimensionalBearbeiten

In drei Dimensionen gibt es vier orthorhombische Bravais-Gitter: primitiv orthorhombisch, basiszentriert orthorhombisch, körperzentriert orthorhombisch und flächenzentriert orthorhombisch.

Bravais-Gitter	Primitiv orthorhombisch	Basis-zentriert Orthorhombisch	Körperzentriert Orthorhombisch	Flächen-zentriert orthorhombisch
Pearson-Symbol	oP	oS	oI	oF
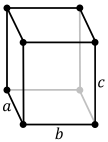
Standardeinheitszelle
Rechtes rhombisches Prisma Einheitszelle

Im orthorhombischen System gibt es eine selten verwendete zweite Wahl der Kristallachsen, die zu einer Einheitszelle mit der Form eines rechten rhombischen Prismas führt; Sie kann konstruiert werden, weil die rechteckige zweidimensionale Grundschicht auch mit rhombischen Achsen beschrieben werden kann. In dieser Achseneinstellung vertauschen das primitive und das basiszentrierte Gitter die Art der Zentrierung, während das Gleiche mit dem körperzentrierten und dem flächenzentrierten Gitter geschieht. Beachten Sie, dass die Länge a {\displaystyle a}

in der unteren Reihe nicht dieselbe ist wie in der oberen Reihe, wie in der Abbildung im Abschnitt über zweidimensionale Verbände zu sehen ist. Für die erste und dritte Spalte oben ist a {\displaystyle a}

der zweiten Reihe gleich a 2 + b 2 {\displaystyle {\sqrt {a^{2}+b^{2}}}}

der ersten Zeile, und für die zweite und vierte Spalte entspricht es der Hälfte davon.