Ortorhombiczny układ krystaliczny

Komórki jednostkowe prostokątne vs rombowe dla sieci ortorhombicznych 2D. Zamiana typu centrowania przy zmianie komórki jednostkowej dotyczy również siatek ortorhombicznych 3D

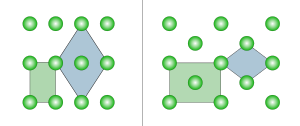
DwuwymiarowyEdit

W dwóch wymiarach istnieją dwie ortorhombiczne siatki Bravais’go: prymitywna prostokątna i wyśrodkowana prostokątna. Prymitywna prostokątna siatka może być również opisana przez centrowaną rombową komórkę jednostkową, podczas gdy centrowana prostokątna siatka może być również opisana przez prymitywną rombową komórkę jednostkową.

TrójwymiarowyEdit

W trzech wymiarach istnieją cztery ortomorficzne siatki Bravais’a: prymitywna ortomorficzna, ortomorficzna ze środkiem w podstawie, ortomorficzna ze środkiem w ciele i ortomorficzna ze środkiem w twarzy.

Siatka Bravaisa	Primitive orthorhombic	Base-centered orthorhombic	Base-centered orthorhombic	Base-centered .centered orthorhombic	Body-centered orthorhombic	Face-centered orthorhombic
Symbol Pearsona	oP	oS	oI	oF
Standardowa komórka jednostkowa
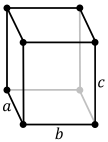Pryzmat rombowy prawy komórka jednostkowa

W układzie ortomorficznym istnieje rzadko stosowany drugi wybór osi krystalicznych, w wyniku którego otrzymuje się komórkę jednostkową o kształcie graniastosłupa prawidłowego rombowego; Można ją skonstruować, ponieważ prostokątna dwuwymiarowa warstwa podstawowa może być również opisana za pomocą osi rombowych. W tym ustawieniu osi, siatki prymitywna i podstawowa zamieniają się typami centrowania, to samo dzieje się z siatkami skupionymi na bryłach i twarzach. Zwróć uwagę, że długość a {

w dolnym rzędzie nie jest taka sama jak w górnym, co widać na rysunku w rozdziale o dwuwymiarowych siatkach. Dla pierwszej i trzeciej kolumny powyżej, a {displaystyle a}

drugiego rzędu równa się a 2 + b 2 {displaystyle {sqrt {a^{2}+b^{2}}}}

pierwszego rzędu, a dla drugiej i czwartej kolumny równa się połowie tego.