Zastosowania algebry

Powiązane tematy:
Więcej lekcji dla GRE Matematyka, Arkusze matematyczne
Ta lekcja jest częścią serii lekcji dla ilościowego rozumowania sekcji GRE poprawionego Testu Ogólnego. W tej lekcji, będziemy się uczyć:

• Zastosowania algebry
• Przekładanie słów na algebrę
• Przykłady użycia algebry do rozwiązywania zadań słownych
  • Średnie zadania słowne
  • Mixture Word Problems
  • Distance, Rate, Time Word Problems
  • Work Word Problems
  • Word Problems that involve Simultaneous Equations
  • Word Problems that involve Inequalities

Zastosowania Algebry
Przekształcanie opisów słownych na wyrażenia algebraiczne jest niezbędnym początkowym krokiem w rozwiązywaniu problemów słownych. oniżej podano kilka przykładów.
– Jeżeli kwadrat liczby x pomnożymy przez 4, a następnie do tego iloczynu dodamy 15, to wynik możemy przedstawić jako 4×2 + 15
– Jeżeli obecna pensja Piotra s zostanie zwiększona o 15 procent, to jego nowa pensja wynosi 1,15s.
– Jeśli y galonów soku pomarańczowego ma zostać rozdzielone między 5 osób w taki sposób, że jedna osoba dostanie 1 galon, a reszta soku zostanie równo podzielona między pozostałe 4 osoby, to każda z tych 4 osób dostanie (y – 1) ÷ 4
Ten film pokazuje, jak przekształcać słowa i wyrażenia w wyrażenia algebraiczne zawierające zmienne.

• Pokaż rozwiązania krok po kroku

Przykłady użycia technik algebraicznych do rozwiązywania zadań słownych
Pokażemy teraz kilka przykładów użycia technik algebraicznych do rozwiązywania zadań słownych. Więcej przykładów problemów słownych algebry można znaleźć tutaj. Przykłady zadań ze średnią

Poniżej podano przykłady zadań, które dotyczą średniej lub średniej arytmetycznej.

Przykład 1:

Ellen uzyskała następujące wyniki na 3 egzaminach: 82, 74 i 90. Jaki wynik musi uzyskać na następnym egzaminie, aby średnia (arytmetyczna) z 4 egzaminów wyniosła 85 punktów?
Niech x oznacza wynik na następnym egzaminie Ellen.
Średnia z 4 egzaminów to

Rozwiązując dla x otrzymujemy

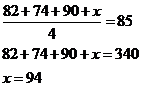
W związku z tym Ellen będzie musiała uzyskać na następnym egzaminie wynik 94.

Przykład 2:

W swoich pierwszych czterech grach Jennifer kręgle 101, 112, 126, 108. Jaki jest minimalny wynik, który musi zdobyć w piątej grze, aby jej średnia wynosiła co najmniej 110?

• Pokaż krok po kroku rozwiązania

Zadania z mieszaninami

Poniżej podano kilka przykładów zadań, które dotyczą mieszanin i stężenia mieszanin.

Przykład 1:
Mieszanina 12 uncji octu i oleju stanowi 40 procent octu, gdzie wszystkie miary są wagowe. Ile uncji oleju należy dodać do mieszaniny, aby uzyskać nową mieszaninę, która ma tylko 25 procent octu? iech x oznacza liczbę uncji oleju, który należy dodać. Wówczas całkowita liczba uncji nowej mieszaniny będzie wynosić 12 + x, a całkowita liczba uncji octu w nowej mieszaninie będzie wynosić (0,40)(12). Ponieważ nowa mieszanina musi mieć 25 procent octu, otrzymujemy

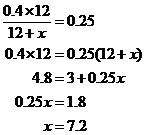
7,2 uncji oleju musi być dodane, aby uzyskać nową mieszaninę, która ma 25 procent octu.

Przykład 2:

Roztwór zawiera 15% kwasu solnego. Ile wody należy dodać do 50 ml tego roztworu, aby rozcieńczyć go do 2% roztworu?

• Pokaż rozwiązanie krok po kroku

Distance, Rate, Time Word Problems

Następujące przykłady to problemy z dystansem, tempem i czasem.

Przykład 1:

W konkursie jazdy Jeff i Dennis przejechali tę samą trasę ze średnimi prędkościami odpowiednio 51 mil na godzinę i 54 mil na godzinę. Jeśli Jeffowi przejechanie trasy zajęło 40 minut, ile czasu zajęło Dennisowi? iech x oznacza czas, w minutach, jaki zajęło Dennisowi przejechanie trasy. Odległość d, w milach, jest równa iloczynowi tempa r, w milach na godzinę, i czasu t, w godzinach; to znaczy d = rt
Zauważ, że ponieważ tempo jest podane w milach na godzinę, konieczne jest wyrażenie czasu w godzinach; na przykład 40 minut równa się godziny.
Korzystając ze wzoru d = rt, możemy otrzymać następującą tabelę.

	Odległość	Stawka	Czas	Czas
Jeff	51 ×
Dennis	54 ×

Ponieważ odległości są równe,

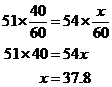
Przejazd kursu zajął Dennisowi około 37.8 minut na przejechanie trasy.

Wprowadzenie do rozwiązywania zadań na temat ruchu jednostajnego (prędkość-czas-odległość) z wykorzystaniem wzoru prędkość x czas = odległość, czyli rt=d.
Przykład:
Dwóch rowerzystów startuje z tego samego rogu i jedzie w przeciwnych kierunkach. Jeden rowerzysta jedzie dwa razy szybciej niż drugi. W ciągu 3 godzin dzieli ich odległość 81 mil. Znajdź tempo jazdy każdego z rowerzystów. Odpowiedź: 9 mph i 18 mph.

• Pokaż rozwiązania krok po kroku

Problem słowny z wykorzystaniem wzoru na ruch jednostajny rt=d
Przykład:
Biegacz rozpoczął bieg ze średnią prędkością 6 mph. Pół godziny później inny biegacz zaczął biec za nim z tego samego miejsca ze średnią prędkością 7 mil na godzinę. Ile czasu zajmie biegaczowi dogonienie biegacza? Odpowiedź: 3 godziny.

• Pokaż rozwiązanie krok po kroku

Problem słowny z zastosowaniem wzoru na ruch jednostajny rt=d
Przykład:
Na 555-milową, 5-godzinną wycieczkę po Autobahn jechano z dwiema prędkościami. Średnia prędkość samochodu wynosiła 105 mph w pierwszej części podróży, a średnia prędkość wynosiła 115 mph w drugiej części. Jak długo samochód jechał z każdą prędkością? Odpowiedź: 105 mph przez 2 godziny i 115 mph przez 3 godziny.

• Pokaż rozwiązanie krok po kroku

Problem słowny z zastosowaniem wzoru na ruch jednostajny rt=d
Przykład: ndrzej i Beth znajdują się na przeciwległych końcach 18-milowej drogi wiejskiej i planują wyruszyć w tym samym czasie, biegnąc w kierunku siebie, aby się spotkać. Andy biegnie z prędkością 7 mph, a Beth z prędkością 5 mph. Po jakim czasie od rozpoczęcia biegu spotkają się? Odpowiedź: 1,5 godziny.

• Pokaż rozwiązania krok po kroku

Przykład:
Samochód i autobus wyruszyły o 14:00 z tego samego miejsca, zmierzając w tym samym kierunku. Średnia prędkość samochodu jest dwa razy większa niż średnia prędkość autobusu. Po 2 godzinach samochód jest 68 mil przed autobusem. Znajdź prędkość autobusu i samochodu. Odpowiedź: Prędkość autobusu: 34 mph; Prędkość samochodu: 68 mph.

• Pokaż rozwiązania krok po kroku

Przykład:
Pilot leciał z jednego miasta do drugiego z prędkością średnio 150 mph. Później poleciał z powrotem do pierwszego miasta z prędkością średnio 100 mph. Całkowity czas lotu wynosił 5 godzin. Jak daleko od siebie są te miasta? Odpowiedź: 300 mil

• Pokaż rozwiązania krok po kroku

Zadania słowne
Poniżej podano przykłady zadań, które dotyczą pracy wykonywanej przez osoby lub maszyny.
Przykład:
Zbieranie czterdziestu buszli jabłek zajmuje Marii dziesięć godzin. Kayla może zebrać tę samą ilość w 12 godzin. Ile czasu zajęłoby im to, gdyby pracowały razem?

• Pokaż rozwiązanie krok po kroku

Problemy słowne związane z pracą
Przykłady:
1. Doświadczony malarz potrzebuje 6 dni, aby pomalować dom. Malowanie tego samego domu zajmuje praktykantowi 8 dni. Ile czasu zajęłoby im to, gdyby pracowali razem?
2. Jedna rura może napełnić zbiornik w 8 godzin. Inna rura może opróżnić zbiornik w ciągu 12 godzin. Jeśli obie rury są otwarte jednocześnie, ile czasu zajmie napełnienie zbiornika?

• Pokaż rozwiązania krok po kroku

Zastosowania, które obejmują układy równań
Poniżej podano przykłady zastosowań, które obejmują układy równań lub rozwiązywanie równań równoczesnych.
Przykłady:
1. Znajdź dwie liczby, dla których suma wynosi 93, a różnica 9.
2. Obwód prostokąta wynosi 160 yd. Szerokość jest o 4 większa niż połowa długości. Znajdź długość i szerokość.
3. Sunset wynajmuje ciężarówkę 18 stóp za 49,95 dolarów plus 75 centów za milę. Cactus wynajmuje 18-stopową furgonetkę za 59,95 dolarów plus 50 centów za milę. Dla jakiego przebiegu koszty są takie same?

• Pokaż krok po kroku rozwiązania

Przykłady:
1. Załóżmy, że wszystkie kursy Pheonix College są warte 3 lub 4 punkty. Drużyna biegowa bierze udział w 40 kursach, które są warte 144 punkty. Ile kursów 3-kredytowych i ile kursów 4-kredytowych jest branych pod uwagę?
2. HomeMart pobiera 3,50$ za żarówkę CFL i Supply Depot pobiera 2,50$ za żarówkę CFL, która nie świeci tak długo. Jeśli twój kompleks apartamentów stracił fakturę, ale wiedzieli, że kupił 300 żarówek i spędził 885 dolarów, ile żarówki zostały zakupione z każdego sklepu.
3. Grounds Works opłaty 8,00 dolarów / funt dla premii kawy palonej i 4,50 dolarów / funt dla wartości kawy palonej. Ile z każdego rodzaju powinny być stosowane do 10lb mieszanki, która będzie kosztować $ 5,90/lb?
4. Pociąg opuścić Prescott, AZ i podróżuje na północ do Grand Canyon z prędkością 25mph. Półtorej godziny później z równoległego toru odjeżdża pociąg ekspresowy, który jedzie na północ z prędkością 60 mph. Jak daleko od stacji początkowej spotkają się?

• Pokaż rozwiązania krok po kroku

Zastosowania, które zawierają nierówności
Następujące przykłady problemów słownych algebry, które zawierają nierówności
Przykłady:
1. Andrea ma 53,50 dolarów w kieszeni i chce kupić koszule w cenie sprzedaży 14,95 dolarów każdy.
Jaka jest największa liczba koszule może kupić? (Załóżmy, że koszule są zwolnione z podatku od sprzedaży)
2. Trzykrotność liczby zwiększonej o 8 wynosi co najwyżej 40. Znajdź największą możliwą wartość tej liczby.
3. Długość pewnego prostokąta jest o 8 metrów mniejsza od pięciokrotności jego szerokości. Jeżeli obwód tego prostokąta wynosi co najwyżej 104 metry, to znajdź największą możliwą szerokość tego prostokąta.
4. Dwie kolejne liczby są takie, że ich suma jest większa od 98 pomniejszonego o dwa razy większą z nich. Znajdź najmniejsze możliwe wartości tych liczb całkowitych.

• Pokaż rozwiązanie krok po kroku

Przykład:
Fabryka widżetów ma stałe koszty operacyjne w wysokości 3600 dolarów dziennie i kosztuje 1,40 dolara za każdy wyprodukowany widżet. Jeśli widget sprzedaje się za $4.20, jaka jest najmniejsza liczba widgetów, które muszą być sprzedane dziennie, aby osiągnąć zysk?

• Pokaż krok po kroku rozwiązania

Wypróbuj darmowy kalkulator matematyczny i rozwiązywanie zadań poniżej, aby ćwiczyć różne tematy matematyczne. Wypróbuj podane przykłady lub wpisz swój własny problem i sprawdź swoją odpowiedź, korzystając z wyjaśnień krok po kroku.