Sistema de cristais ortopédicos

Células de unidade rectangular vs rômbica para as redes ortopombicas 2D. A troca do tipo de centralização quando a célula da unidade é mudada também se aplica para as lattices ortopombicas 3D

Two-dimensionalEdit

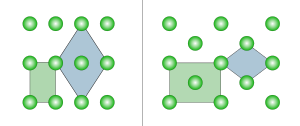
Em duas dimensões existem duas lattices ortopombicas Bravais: rectangulares primitivas e rectangulares centradas. A malha rectangular primitiva também pode ser descrita por uma célula rômbica centrada, enquanto a malha rectangular centrada também pode ser descrita por uma célula rômbica primitiva.

Editar tridimensional

Em três dimensões, existem quatro grelhas Bravais ortopédicas: ortopédica primitiva, ortopédica centrada na base, ortopédica centrada no corpo, e ortopédica centrada na face.

b>centrado no corpo
orthorhombic

Bravais lattice	Primitive orhombic	Base-centrado orthorhombic	Face-centrered orthorhombic
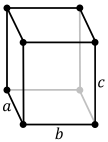
oP	oS	oI	oF
Célula de unidade padrão
Prisma rômbico direito unit cell	Prisma rômbico direito, centrado em base

No sistema ortopédico há uma segunda escolha raramente utilizada de eixos de cristal que resulta numa célula unitária com a forma de um prisma rômbico direito; pode ser construída porque a camada base bidimensional rectangular também pode ser descrita com eixos rômbicos. Neste ajuste de eixos, as estruturas primitivas e centradas na base trocam em tipo centrado, enquanto o mesmo acontece com as estruturas centradas no corpo e centradas na face. Note-se que o comprimento de um {\\displaystyle a}

na linha inferior não é o mesmo que na linha superior, como se pode ver na figura da secção sobre as lattices bidimensionais. Para a primeira e terceira colunas acima, um {\i1}div> da segunda linha é igual a 2 + b 2 {\i1}displaystyle {\i}{a^{2}+b^{2}}}}

da primeira linha, e para a segunda e quarta coluna é igual a metade disto.