MathématiquesPrécalculs Mathématiques au Nebraska
SectionÉtirements et compressions horizontaux
Dans la section précédente, nous avons discuté du résultat de la multiplication de la sortie de la fonction par une valeur constante. Cependant, que se passe-t-il lorsque nous multiplions l’entrée de la fonction ? Pour explorer cette idée, nous examinons les graphes de
et discutons de la façon dont ils sont liés.
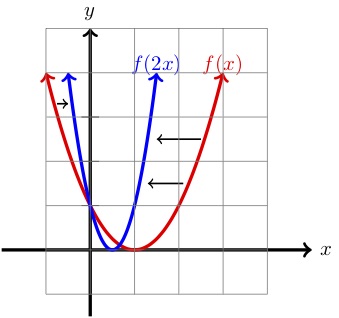
| \(x\) | \(y=f(x)\) | \(y=f(2x)\) | |
| \(-1\) | \(4\) | \(8\) | |
| (-.5\) | \(2.25\) | \(4\) | |
| (0\) | \(1\) | (1\) | \(.5\) | \(.25\) | \(0\) | (1\) | (0\) | (1\) | (2\) | \(1\) | (9\) |
Comme nous pouvons le voir ci-dessus, comparé au graphe de \(f(x)\text{,}\N-) le graphe de \(f(2x) \N-) est compressé horizontalement par un facteur de \N-(2 \N-).En effet, si l’on nous donne un point \((x,y) \) sur le graphe de \(f(x) \) alors \(\left(\dfrac{1}{2}x,y\right) \) est un point sur le graphe de \(f(2x)\text{.}\)
En regardant le tableau ci-dessus, nous pouvons vérifier cela pour quelques points. Par exemple, le point \((2,1)\) est sur le graphe de \(f(x)\text{.}\). Alors
est un point sur le graphe de \(f(2x)\text{.}\)
Extension horizontale
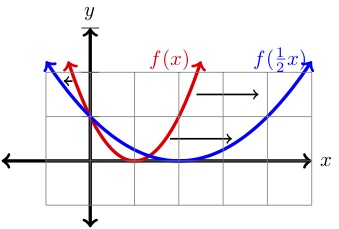
| \N(x) | \N(y=f(x)\) | (y=f\left(\dfrac{1}{2}xright)\) | |
| \N(-1\) | \(4\) | \(2.25\) | (0\) | (1\) | (1\) | (1\) | (0\) | \(.25\) | (2\) | (1\) | (0\) | (4\) | (9\) | \(1\) |
Le graphe de \(f\left(\dfrac{1}{2}x\\right)\) est étiré horizontalement d’un facteur de \(2 \) par rapport au graphe de \(f(x) \text{.}\) De plus, si \((x,y) \) est un point sur le graphe de \(f(x)\text{,}\) alors \((2x,y) \) est un point sur le graphe de \(f\left(\dfrac{1}{2}x\right)\text{.}\)
Nous pouvons voir cela se jouer dans notre exemple ci-dessus. Remarquez que \((2,1) \) est un point sur \(f(x)\text{,}\) et
est un point sur le graphe de \(f\left(\dfrac{1}{2}x\right)\) comme le montre le tableau et le graphe ci-dessus. En général, on a :
Étirements, compressions et réflexions horizontales
Par rapport au graphe de \(y = f (x)\text{,}\) le graphe de \(y = f (a\cdot x)\text{,}\) où \(a \ne 0\text{,}\) est
- compressé horizontalement par un facteur de \(\abs{a}\) si \(\abs{a}\gt 1\text{,})
- étiré horizontalement d’un facteur de \(\abs{\dfrac{1}{a}}\) si \(0\lt\abs{a}\lt 1\text{,}\) et
- réfléchi autour de l’axe \(y\) (et étiré ou comprimé) si \(a\lt 0\text{.})
Comme vous avez pu le remarquer à ce jour à travers nos exemples, un étirement ou une compression horizontale ne changera jamais les intercepts \(y\). C’est un bon moyen de savoir si une telle transformation a eu lieu.
Exemple272
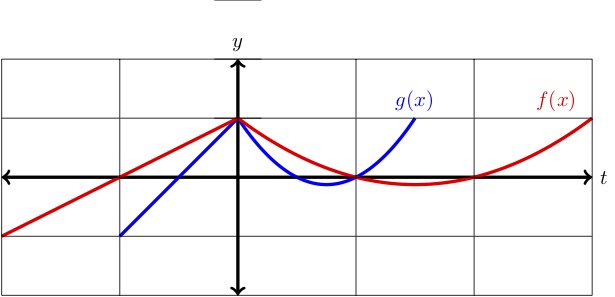
.
Le graphique de \(f(x)\) est représenté avec un étirement horizontal ou une compression de \(f(x) \text{.}\) Décidez si \(g(x) \) est un étirement ou une compression, et donnez une formule pour \(g(x)\) en termes de \(f(x)\text{. }}.}\)
Premièrement, remarquez que l’ordonnée à l’origine (y) reste fixe alors que les ordonnées à l’origine (x) se rapprochent de l’axe (y). Cela nous indique que la courbe \(g(x)\) est une compression horizontale. Les ordonnées de \(x \)-intercepts de \(f(x)\) sont \(x=-1,1,2 \) tandis que les ordonnées de \(x\)-intercepts de \(g(x)\) sont \(x=-.5,.5,1\text{..}.
Donc, les \(x\)-intercepts de \(g(x) \) peuvent être obtenus en prenant les intercepts de \(f(x) \) et en divisant chacun par 2. Cela nous indique que \(g(x)\) est une compression horizontale par un facteur de \(2 \text{..}.}\) Par conséquent, nous pouvons écrire